3.エポキシ樹脂

3.4 2液型エポキシ樹脂塗膜の網目構造とその解析

3.4.1　原料組成から見た網目構造

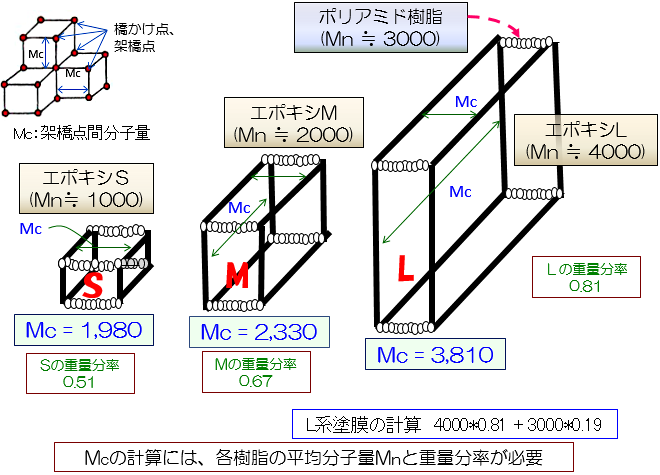
 　前回の図5-30に示すポリアミド樹脂を固定し、エポキシ当量が一連に異なるＳ、Ｍ、Ｌを使用した塗膜の網目構造は、どのようになるのかを考えて見る。前回の図5-31には、エポキシ樹脂SとＬをそれぞれに使用した塗膜の網目密度の違いを表した。全ての架橋点が網目を形成すると考えると、エポキシ当量の小さいＳ系塗膜の方が緻密な網目を形成する。Ｓ、Ｍ、Ｌ系塗膜の網目構造を抽出すると、図5-32で示され、さらにエポキシとポリアミド樹脂の配合(混合)割合から架橋点間分子量（橋かけ点間の平均分子量）M_cが計算できる。計算結果は表5-4に示すように、塗膜のM_cが小さくなるほど細かな網目（網目密度大）を形成している。このような分子論的な微細な網目密度の差異を実際に測定できるかどうかを考えるだけでも興味をそそる。どのように考え、実測するのかを今回の主題とする。ここで取り上げた塗膜は原料と組成が比較的明らかであり、網目構造の違いを考えるモデルとして相応しい。そして、ここに示す2液型塗料は常温でも硬化反応するが、硬化条件を追試できるように120℃/30分で焼付けた。

3.4.2　M_cの実測方法

 　一般に、橋かけ塗膜（クッキー）の物性はM_cとどのような関係があるだろうか。分子間引力から解放されて大きな分子運動ができるゴム状態になって初めて、クッキーの物性はM_cに支配される。とりわけ、ゴム状態におけるヤング率（引張り弾性率でE_rと表す）は網目密度の大きさを表す1/M_cと相関し、M_cが小さいほど網目が細かくなり（網目密度大）、ヤング率E_rは大きくなる。では、実際にM_cを測定してみよう。

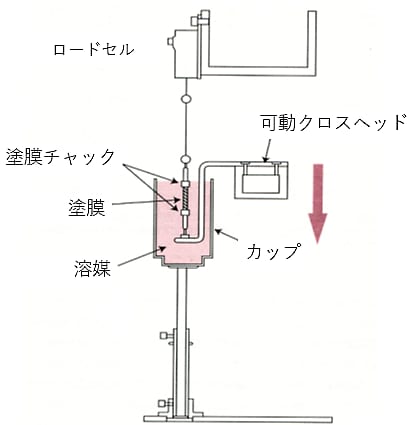
塗膜を図5-33に示すように良溶媒中に浸漬すると、所定温度で平衡膨潤状態になる。クッキーだからできる引張り試験であり、膨潤時のヤング率E_rを測定し、このE_rを次式に代入してM_cを求める。^7）

M_c = 3ρRT/ E_r　(3)

 　ここで、ρ：塗膜の密度〔g/cm³〕、ρ=1.2を用いた、R=8.31〔J/K・mol〕、T：膨潤時の浸せき温度〔K〕、E_r: 膨潤状態における弾性率 〔Pa= N/m²〕 。
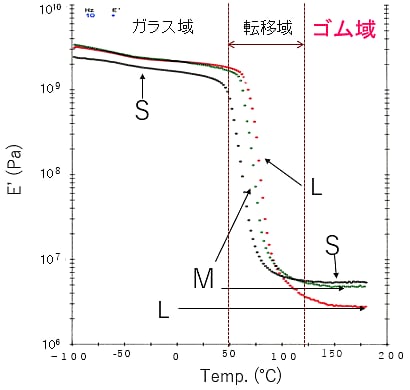
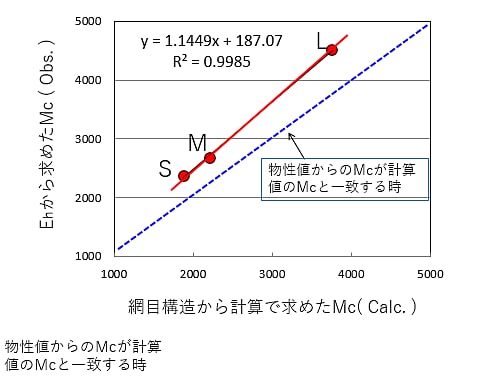
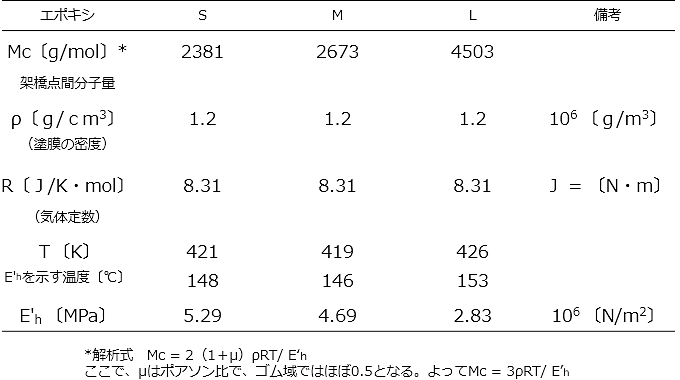
 　(3)式より、E_rが大きいほど、M_cが小さくなり、網目密度が高くなる。膨潤状態はゴム状態と同じであり、E_r はTg以上（ゴム域）における弾性率に相当する。現在では、膨潤引張り測定の代わりに、図5-34に示す動的粘弾性測定装置を使用し、温度分散曲線を測定することが圧倒的に多い。Ｓ、Ｍ、Ｌ系塗膜の動的弾性率E'の温度分散曲線を図5-35に示す。ゴム域におけるE'は150℃付近で最小値E'_hを示す。このE'_h値はＳ、Ｍ、Ｌ系塗膜の順に小さくなった。(3)式のE_rにE'_h値を代入してM_cを求めた。計算結果を前回の表5-4に示す。さらに、網目構造から計算で求めたM_c と物性測定から求めたM_cとの相関性を図5-36に示す。これらの結果より、今回使用した2液型エポキシ樹脂塗膜は予測通りの橋かけ構造を形成していることが認められた。また、図5-36のデーターからM_cの実測値が計算値のそれよりも大きいことは、架橋点が100%反応していないことを示している。なお、物理的定義に従うゴム弾性率は図5-37に示す絶対温度0Kへの外挿値であるが、ここではE'_h値で代用した。M_cの計算に必要な物性値を表5-5にまとめて示す。注意すべき点は、顔料や充てん材を練入した塗膜のE'_hを使用してはいけないことである。剛体粒子の充てんによるE'_hの上昇を計算で除くのは難しいので、測定にはクリヤ塗膜に限る。

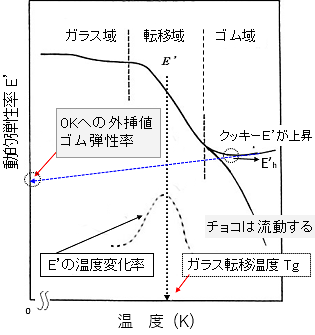
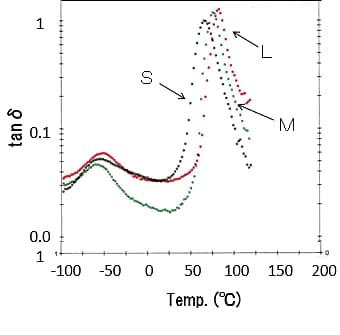
表5-5　M_cを求めるために必要な物性値

3.4.3　塗膜のTgに及ぼす橋かけ密度の考察

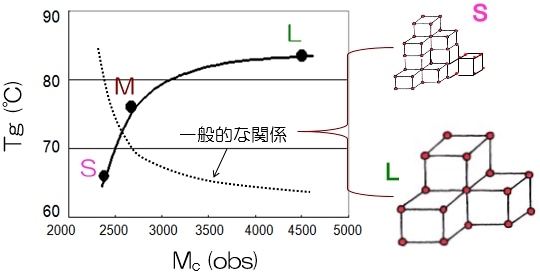
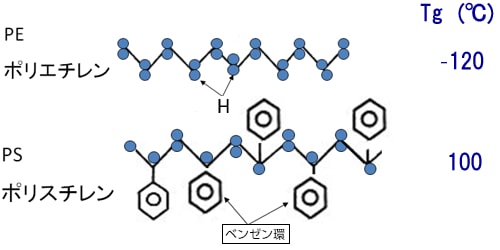
 　ジャングルジムの形成はポリマー分子鎖の運動性を束縛するのでガラス転移温度Tgを上昇させる。Tgとは、図5-37に示すように、ガラス状態からゴム状態に転移する中間温度で、熱変形温度や耐熱性の目安になる。図5-37に示すE'～温度曲線の変化率からTgを求めてもよいが、動的粘弾性測定では、動的損失tanδまたは動的粘性率E"の温度曲線が得られ、この曲線のピーク温度をTgと見なすことができる。著者は塗膜のtanδ～温度曲線のピーク温度からTgを求めている。図5-35のE'と同様に、2液型エポキシ樹脂塗膜のtanδ～温度曲線を図5-38に示す。さらに、tanδピーク温度から求めたTgとE'_h値から求めたM_cとの関係を図5-39に示す。TgはM_cの増大に伴い上昇した。これは、一般のクッキー塗膜で観察される現象と相反する結果である。TgとM_cとの関係について考察する。図5-32に示すように、エポキシとポリアミド樹脂で形成される網目は、硬い分子鎖と軟らかい分子鎖からできており、網目にどちらの分子鎖が多く組み込まれるかがKey point になる。Ｓ、Ｍ、Ｌの順に橋かけ点間に含まれるベンゼン環は多くなる。図5-40に示すPEとPSのように、メチレン結合の側鎖がHからベンゼン環に変わるだけでTgは-120℃から100℃に劇的に上昇する。よって、図5-39の結果は図5-40に示す分子鎖の熱運動性の違いを反映しており、分子鎖の可動性効果の方が橋かけ密度の効果を上回っていることを示している。

本レポートで明らかにしたかった点は次の3点であり、それぞれについてコメントする。

Ｑ１：物性測定からM_cが求まるのか。
Ａ１：M_cを求めることができる。遊離塗膜の動的粘弾性の温度依存性を測定し、ゴム域のE'の最小値E'_hを求め、ゴム弾性理論式に代入すればよい。

Ｑ２：網目構造から計算で求めたM_cと物性測定から求めたM_cとは相関するか。
Ａ２：相関するが、完全に一致しない。物性測定から求めたM_cは計算値よりも若干、大きかった。

Ｑ３：塗膜のTgは橋かけが緻密になる（M_cが小さくなる）ほど、上昇するのか。
Ａ３：一般的にはこの考え方で良いが、エポキシ樹脂塗膜では樹脂特有の分子構造（ベンゼン環）の影響を考える必要がある。網目を形成する分子鎖の動き易さが橋かけ密度の効果を上回ることがある。

『塗料・塗装の何でも質問講座』の目次